
Como avaliar a desvalorização do seu carro?
By Neale Ahmed El-Dash on Oct 4, 2019
Nesse post discutiremos a dinâmica da desvalorização dos carros no mercado brasileiro. Além de considerar o modelo e a idade do carro como é feito nas estimativas de preço da tabela FIPE, também iremos avaliar a importância da quilometragem. Ao final do post, apresentaremos um ranking preliminar da desvalorização média das marcas de carro mais populares do Brasil.
Introdução
Em 1973, a Fundação Instituto de Pesquisas Econômicas (FIPE) criou uma tabela dos preços de carros, que é a principal referência de preço no mercado de carros usados e seminovos no país. Essa tabela, chamda tabela FIPE, é atualizada mensalmente, sendo que suas estimativas são baseadas nos preços amostrados de carros, motos e caminhões usados, seminovos e novos no mercado nacional. Essas estimativas são publicadas por Marca/Modelo do carro e ano de fabricação do veículo. O modelo do veículo inclui informações como tipo de câmbio, potência/motor, combustível e número de portas. No site da FIPE, a tabela é descrita como sendo:
“A Tabela Fipe expressa preços médios de veículos anunciados pelos vendedores, no mercado nacional, servindo apenas como um parâmetro para negociações ou avaliações. Os preços efetivamente praticados variam em função da região, conservação, cor, acessórios ou qualquer outro fator que possa influenciar as condições de oferta e procura por um veículo específico.”
No mesmo site, também é disponibilizado um vídeo animado, descrevendo como as estimativas da tabela FIPE são produzidas. Esse vídeo pode ser visto abaixo.
Eu sempre comprei carros semi-novos, que são carros usados porém com uma quilometragem (km) baixa. É uma questão de gosto pessoal; não dou muito valor a carros. Somente quero algo em bom estado de conservação, porém sem gastar muito. Quando compramos carros usados, sempre há uma negociação, tanto do carro que você deseja comprar, quanto do seu carro velho que você provavelmente quer incluir na transação. E nessas negociações, usualmente a tabela FIPE é utilizada como referência.
A última vez que comprei um carro foi em 2016. Comprei um Hyundai i30, ano 2012, com 39 mil km rodados. E nessa negociação senti muita falta de informação para poder ajustar os valores da tabela FIPE de acordo com a quilometragem do carro. Queria ter uma estimativa mais precisa do valor do carro que eu estava comprando. Com certeza um i30 de 2012 com 40 mil km rodados devia ser mais barato que um com 30 mil km rodados. Minha grande dúvida era saber quão mais barato o carro deveria ser. E a tabela FIPE não ajuda nessa questão, nem informando qual a média de km rodados para veículos de um determinado ano, nem ajustando os preços pela quilometragem do carro. Sem falar em outros fatores que podem afetar os preços, como estado de origem, opcionais e lataria, bem como se teve apenas um dono, se é financiado, se a documentação está regularizada, se a revisão foi feita na concessionária, etc…
Mesmo depois que comprei o carro mencionado acima, continuei pensando sobre o assunto. Como poderiam ser ajustadas as estimativas da tabela FIPE, considerando outros fatores relevantes para determinar o preço? Minha solução foi baixar todas as ofertas de carros de um site especializado, adicionar a esses dados as estimativas de preço da tabela FIPE, e depois fazer um modelo onde o preço do carro depende não só do valor da tabela FIPE, mas também dos outros fatores mencionados acima.
Dentro de algumas semanas, o site Polling Data irá publicar esse modelo. Ele ainda está em desenvolvimento, porém os dados já foram coletados. Preliminarmente, estamos trabalhando com os dados da tabela FIPE de Jun/2019 e com todos os carros anunciados no site Mercado Livre até o dia 10/09/2019, porém depois de desenvolvido, o modelo será atualizado mensalmente.
Como o modelo ainda não está pronto, minha ideia para esse post é fazer uma análise descritiva dos dados, focando na depreciação do valor dos carros em função apenas da quilometragem dos mesmos. Qual será a marca que tem, em média, a menor depreciação no mercado nacional? Para responder a essa pergunta, ao final desse post faremos um ranking nacional de depreciação das marcas de veículos.
Validação dos dados do Mercado Livre
Para quem trabalha com estatística ou computação, o termo “Big Data” é cada vez mais popular. Existem várias definições sobre o significado desse termo. Algumas são relativamente superficiais, focando apenas na ideia de que são conjuntos de dados grandes demais para serem analisados utilizando ferramentas tradicionais de análise de dados, mas não gosto dessa definição porque ela foca somente em uma dimensão da questão.
Por enquanto, a definição que mais me agrada descreve o termo com relação as seguintes características: Volume, Variedade, Velocidade e Validade. Essas são conhecidas como os 4V’s. Existem outras definições com mais V’s, porém esses quatro já são suficientes do meu ponto de vista. Cada V é explicado abaixo:
- Volume: Grande volume de dados.
- Variedade: Dados de diferentes fontes e/ou formatos.
- Velocidade: Dados que se alteram ou são atualizados frequentemente.
- Validade: Dados que podem ser validados por algum benchmark externo.
Note que na minha definição, o Volume não implica que os dados não possam ser analisados por ferramentas tracionais. Entendo que bases de dados que se encaixem em pelo menos dois dos V’s acima já podem ser denomidadas de Big Data. Os dados citados acima se encaixam nos três primeiros V’s. São duas fontes de dados diferentes, sendo mais de 24 mil preços da FIPE e 150 mil anúncios de carros do Mercado Livre. Além disso, novos anúncios são feitos todos os dias, e os preços da FIPE atualizados todo mês. Porém, o motivo que me levou a citar essa definição de Big Data com 4V’s não foram os três primeiros V’s, e sim o último V: Validade. Esse é o V mais importante do meu ponto de vista.
Nesse caso específico dos anúncios de carros, a validação dos dados se refere essencialmente em verificar/garantir que os anúncios considerados na análise sejam “reais”, tanto no aspecto de não ser uma oferta falsa, quanto no de ser um valor plausível para o carro. Para validar esses dados, o primeiro passo foi compatibilizar os dados da tabela FIPE com os dos anúncios, principalmente no que diz respeito a Marca/Modelo dos veículos. A forma como a tabela FIPE identifica o modelo de carro é bem específica, porém cada anunciante descreve o modelo do seu carro da forma que quer. Não é uma tarefa trivial identificar para cada anúncio publicado qual é o modelo da tabela FIPE a que ele se refere.
Após essa compatibilização, é possível comparar os preços anunciados com os preços de referência da tabela FIPE. Apesar de esperar diferenças entre esses preços, o que motivou a criação de um novo modelo, não esperamos diferenças absurdas. Aqui, a etapa de validação consiste em limpar a base de dados, de forma que apenas anúncios que não refletem diferenças absurdas entre o preço anunciado e o preço da FIPE serão mantidos na análise. Dessa forma, esperamos ter retirado tanto anúncios exgerados ou com erros, quanto também evitado erros de compatibilização devido ao processo descrito acima.
Claramente, o critério para manter um anúncio na base de dados é subjetivo. Os critérios utilizados para analisar os dados nesse post foram: Carros com mais de 5.000 km e menos de 250.000 km rodados com preço anunciado entre R$ 2.000 e R$ 150.000, como também carros no qual a diferença absoluta percentual entre o preço da FIPE e o anunciado no site não excedia 30%. O objetivo desses filtros foi, além de garantir a validade dos anúncios , definir o universo de carros usados, com preços e quilometragem limitados a valores que considero razoáveis para o público que terá interesse em utilizar o modelo.
Como passo final da validação faremos uma análise descritiva simples. No gráfico 1 comparamos o preço médio da tabela FIPE com o valor anunciado dos carros, para cada faixa de 5 mil km rodados. As médias de preços para carros nessas faixas são muito parecidas, quase sobrepostas, mostrando que os preços anunciados são compatíveis aos da tabela FIPE. A correlação linear entre os dois preços é de 0,99. A importância dessa comparação mostrada no gráfico abaixo é que ela leva em consideração as variáveis mais relevantes para análise que será feita no post: o preço, a quilometragem e, implicitamente, a marca/modelo do carro.
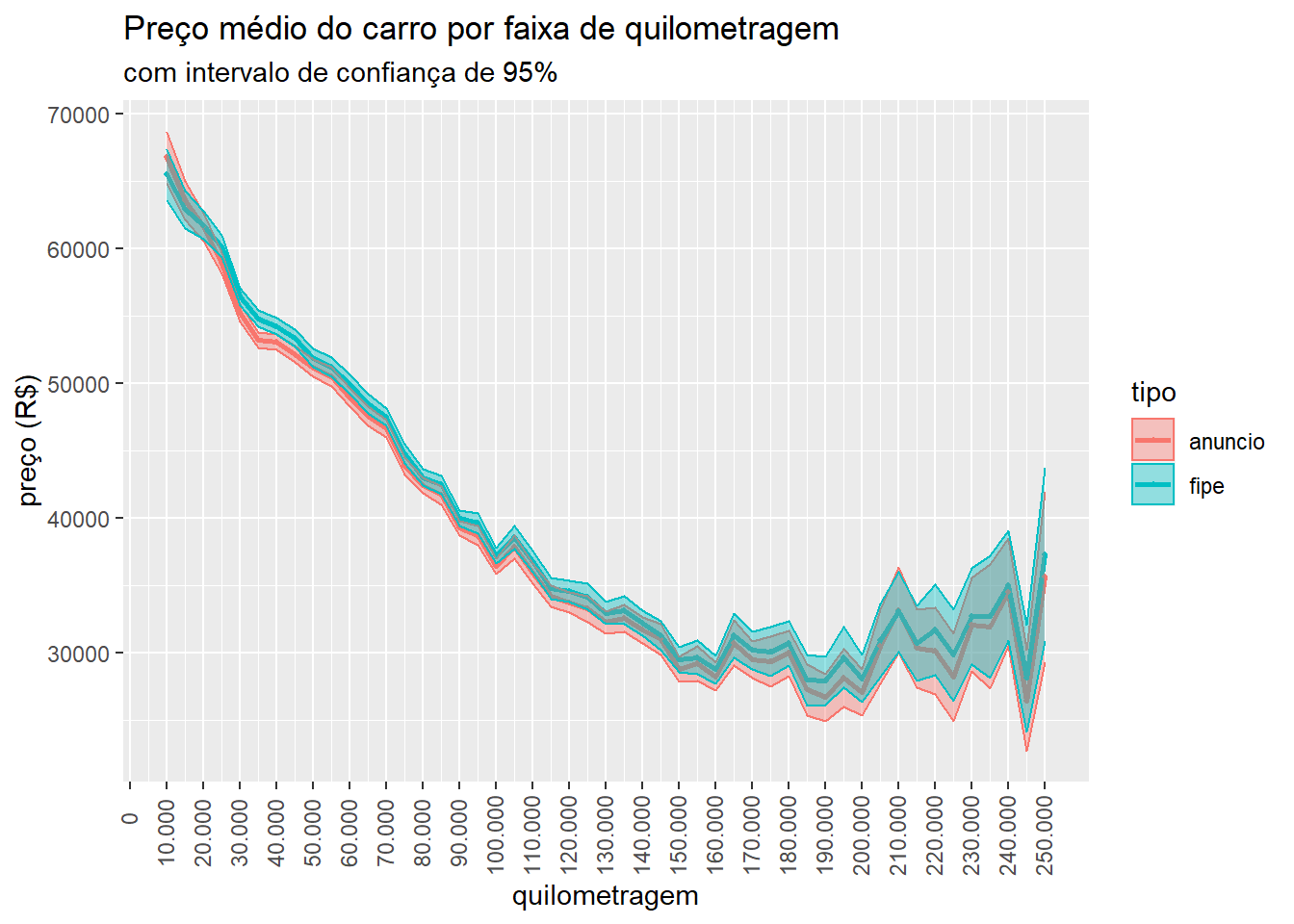
Figure 1: Comparação dos preços anunciados com os preços da tabela FIPE
Dados dos anúncios
Como essa é uma análise preliminar dos dados dos anúncios, ainda não vou escrever sobre como esses dados foram extraídos da internet, nem sobre como as bases de dados de preços da tabela FIPE e dos carros anunciados no site Mercado Livre foram compatibilizadas. Por enquanto vou apenas disponibilizar a base de dados utilizada, a qual está no formato rds e pode ser baixada nesse link.
dir = tempdir()
#código baixando os dados do site do PollingData
url <- "http://www.pollingdata.com.br/blog/desvalorizacao carro - 03-10-2019/df_post.rds"
file.data = tempfile(tmpdir=dir, fileext=".rds")
download.file(url,file.data,method="curl")
df.post <- readRDS(file.data)
#definindo função ci utilizada para calcular os intervalos de confiança
ci <- function(x){1.96*sqrt(var(x,na.rm = TRUE)/length(x))}
#criando as faixas de quilometragem
df.bars.tot <- df.post %>% mutate(
km.fx = cut(km,breaks = seq(0,250000,by = 5000),labels = seq(5000,250000,by = 5000), include.lowest = FALSE)
)
#calculando as estatísticas para cada faixa de quilometragem
df.bars.tot <- df.bars.tot %>% group_by(km.fx) %>% summarise(
n = n(),
ci.fipe = ci(preco.fipe),
media.fipe = mean(preco.fipe,na.rm = TRUE),
ci.anuncio = ci(preco),
media.anuncio = mean(preco,na.rm = TRUE)
)
df.bars.tot <- df.bars.tot %>% gather(stat,val,starts_with('ci'),starts_with('media'))
df.bars.tot$tipo <- str_extract(df.bars.tot$stat,'(?<=\\.).*$')
df.bars.tot$stat <- str_extract(df.bars.tot$stat,'^.*(?=\\.)')
df.bars.tot <- df.bars.tot %>% spread(stat,val)
df.bars.tot$km.fx <- as.numeric(as.character(df.bars.tot$km.fx))
#criando o gráfico
gg.tot <- ggplot(df.bars.tot) +
geom_line(aes(x=km.fx, y=media,colour=tipo,group=tipo),size = 1)+
geom_point(aes(x=km.fx, y=media,colour=tipo),size=0.8) +
geom_ribbon(aes(x=km.fx,ymin=media-ci,ymax=media+ci,fill=tipo,colour=tipo),alpha=0.4) +
scale_x_continuous(name="quilometragem", breaks = seq(0,250000,by = 10000),labels=format(seq(0,250000,by = 10000),digits=0,big.mark=".",decimal.mark=",",scientific = FALSE),minor_breaks = seq(0,250000,by = 5000)) +
labs(title = "Preço médio do carro por faixa de quilometragem",
subtitle = "com intervalo de confiança de 95%") + ylab("preço (R$)") +
theme(axis.text.x = element_text(angle = 90, vjust=0.4))
gg.totUm ponto importante desse post é a utilização da quilometragem como principal fator de depreciação do preço do carro. Na tabela FIPE, como mencionado anteriormente, além do modelo do carro, o único fator de depreciação de um veículo é o ano de fabricação. Para mostrar como não somente o ano de fabricação, mas também a quilometragem, é importante, desenhamos o gráfico 2. Nele é possível ver que, para cada ano, existe uma grande variação da quilometragem entre os carros. Em média, a amplitude de variação é maior do que 50.000 km. Ou seja, dentro de uma idade específica, existem carros com uma grande variação de km rodados. Isso sugere que levando em conta não somente o ano de fabricação, mas também a quilometragem, deve resultar numa estimativa de valor mais precisa.

Figure 2: Intervalo de variação da quilometragem de acordo com a idade do carro
Amplitude por idade
Para gerar esse gráfico, utilizamos a mesma base de dados da seção original, porém ela é manipulada de forma diferente. Nesse gráfico, apesar de só haver um tipo de dado, mantive o mapeamento da variável tipo na definição do gráfico, para forçar a criação da legenda. Fiz isso apenas para deixar claro que nesse gráfico estamos analisando somente os preços dos anúncios, e não os preços da tabela FIPE.
#calculando idade dos carros e aplicando filtros
df.bars <- df.post %>% mutate(
idade = 2019 - as.numeric(ano_modelo)
)%>% filter(km <= 150000, idade <= 20)
#calculando as estatísticas para cada idade
df.bars <- df.bars %>% group_by(idade) %>% summarise(
n = n(),
ci1.anuncio = quantile(km,probs = 0.1),
ci2.anuncio = quantile(km,probs = 0.9),
media.anuncio = mean(km,na.rm = TRUE)
)
df.bars <- df.bars %>% gather(stat,val,starts_with('ci'),starts_with('media'))
df.bars$tipo <- str_extract(df.bars$stat,'(?<=\\.).*$')
df.bars$stat <- str_extract(df.bars$stat,'^.*(?=\\.)')
df.bars <- df.bars %>% spread(stat,val)
#criando o gráfico
gg.post4 <- ggplot(df.bars %>% filter(tipo %in% c("anuncio"))) +
geom_line(aes(x=idade, y=media,colour=tipo,group=tipo),size = 1)+
geom_point(aes(x=idade, y=media,colour=tipo),size=0.8) +
geom_ribbon(aes(x=idade,ymin=ci1,ymax=ci2,fill=tipo,colour=tipo),alpha=0.4) +
labs(title = "Relação entre quilometragem e Idade do veículo",
subtitle = "Intervalo utilizando 1º e 9º decis") + ylab("quilometragem (km)") + xlab("Idade do veículo") +
theme(axis.text.x = element_text(angle = 90, vjust=0.4))
gg.post4Indicador de depreciação do carro
Já ouvi muitas pessoas dizerem que os carros se desvalorizam muito nos primeiros anos ou kms de vida. Também é comum ouvir que quando os carros atingem 100.000 km o preço deles diminui muito; então é melhor vender antes disso. Podemos avaliar a plausabilidade dessas afirmações usando o gráfico 3, onde a quilometragem foi dividida em 4 faixas disjuntas (“Menos de 30.000 km”, “De 30.000 a 110.000 km”, “De 110.000 a 150.000 km”, “Mais de 150.000 km”). Como esta é uma análise preliminar, não usamos nenhuma técnica estatística para detectar mudanças estruturais e identificar essas faixas. Elas foram criadas baseadas numa simples análise visual dos dados.

Figure 3: Faixas de desvalorização dos carros anunciados
Depreciação por faixa
Para gerar esse gráfico, utilizamos a mesma lógica da criação do primeiro gráfico. A principal diferença é criar um variável chamada faixas, a qual será utilizada para criar o grid no gráfico, o qual particiona o mesmo em quatro grupos de faixas de quilometragem.
#criando faixas de quilometragem para particionar o gráfico
df.bars.tot$faixas <- cut(df.bars.tot$km.fx,breaks = c(0,30000,110000,150000,250000),labels = c('<30k km','30k-110k km','110k-150k km','Mais de 150k km'))
#gerando o gráfico.
gg.tot2 <- ggplot(filter(df.bars.tot,tipo == "anuncio")) +
geom_line(aes(x=km.fx, y=media,colour=tipo,group=tipo),size = 1)+
geom_point(aes(x=km.fx, y=media,colour=tipo),size=0.8) +
geom_ribbon(aes(x=km.fx,ymin=media-ci,ymax=media+ci,fill=tipo,colour=tipo),alpha=0.4) +
geom_smooth(aes(x=km.fx, y=media),method = "lm", size = 1, colour="darkblue",se = FALSE,linetype = "dashed") +
facet_grid(.~faixas,scales="free_x",space="free_x") +
scale_x_continuous(name="quilometragem", breaks = seq(0,250000,by = 10000),labels=format(seq(0,250000,by = 10000),digits=0,big.mark=".",decimal.mark=",",scientific = FALSE),minor_breaks = seq(0,250000,by = 5000)) +
labs(title = "Preço médio do carro por faixa de quilometragem") + ylab("preço (R$)") +
theme(axis.text.x = element_text(angle = 90, vjust=0.4))
gg.tot2Me parece que o fato de maior destaque no gráfico é que há um decréscimo gradual no valor do carro até atingir 150.000 km rodados. Depois desse ponto, parece que a quilometragem do carro não afeta mais o valor do carro. Vale a ressalva de que nessas quilometragens mais altas o intervalo de confiança para a média aumenta progressivamente. Isso é um indicativo de que os preços oscilam mais, como também de que não existem tantos carros com esse perfil na base de dados. Ou seja, existe mais incerteza sobre os preços praticados em carros muito rodados (mais de 150.000 km) do que em carros menos rodados.
Com relação as outras três faixas, de fato parecem haver algumas mundanças na velocidade de decrescimento do valor do carro. Para evidenciar essas diferenças, adicionamos as linhas pontilhadas ao gráfico. Essas linhas foram geradas por um modelo de regressão linear simples que modela o preço em função da quilometragem. Como estamos fazendo apenas uma análise visual do gráfico, não me preocupei em mostrar a inclinação da reta. Porém, na primeira faixa (Até 30.000 km) o decréscimo do valor do carro é mais rápido que na faixa seguinte (De 30.000 a 100.000 km), na qual, por sua vez, o decréscimo também é um pouco mais íngrime do que na terceira faixa (De 100.000 a 150.000 km). Ou seja, há índicios de que de fato, nos primeiros 30 mil km rodados, o valor do carro deprecia mais rapidamente. Já com relação à segunda afirmação, a realidade é outra. Depois dos 110 mil km, a velocidade do decréscimo do valor se reduz, essencialmente deixando de ocorrer após 150 mil km.
Com base nesses resultados, podemos definir um indicador de depreciação como sendo a razão dos preços médios do mercado no início (+/- 10.000 km) e no final (+/- 150.000 km) desse intervalo de descrescimento do preço dos carros. Quanto menor for o indicador, maior a depreciação. Matematicamente, esse indicador é definido como:
Depreciação =valor médio mercado faixa de 145.000 km a 155.000 kmvalor médio mercado faixa de 5.000 km a 15.000 km.
Utilizando esse indicador, a depreciação média do mercado, após quase 150.000 km é de 2879866782=43%. Ou seja, nesse intervalo um carro perde, em média, mais de metade do seu valor. Pensando de outra forma, podemos dizer que em média, a cada 10.000 km rodados, um carro perde 3% do seu valor.
Depreciação por marca de carro
Nessa seção iremos calcular o indicador de depreciação, como definido na seção anterior, para as 16 marcas mais populares do país. No gráfico 4, replicamos o gráfico da seção anterior, porém agora por marca e com limitação à quilometragem de 150.000 Km rodados. Nesse gráfico é fácil perceber que marcas mais caras e importadas, como BMW e Audi têm uma depreciação média maior que outras marcas, além de também terem uma margem de erro maior associada ao preço médio delas. Isso talvez se deva à amostra pequena, como também à grande variabilidade de preço entre os modelos dessas marca. As marcas Honda e Toyota têm a fama de serem as marcas que menos desvalorizam, porém no gráfico essa vantagem competitiva parece pertencer somente à Toyota.

Figure 4: Desvalorização média dos carros por marca
Depreciação por marca
A base de dados utilizada para criar esse gráfico é a mesma, porém a base de anúncios é filtrada para manter apenas as 16 marcas de veículos mais populares do país. Para gerar esse gráfico, utilizamos a mesma lógica da criação do gráfico anterior. A principal diferença é utilizar a variável marca para gerar o grid no gráfico.
# calculando quantos veículos são anunciados por marcas/ano
df.marcas <- df.post %>% group_by(marca,ano_modelo) %>% count()
df.marcas <- df.marcas %>% spread(ano_modelo,n)
df.marcas$tot <- rowSums(df.marcas[,-1],na.rm = TRUE)
df.marcas <- df.marcas %>% arrange(desc(tot))
#identificando quais são as 16 principais marcas de veículos do país
marcas.in <- df.marcas$marca[1:16]
# criando as faixas de quilometragem e filtrando base para manter apenas as 16 marcas acima
df.bars <- df.post %>% mutate(
km.fx = cut(km,breaks = seq(0,250000,by = 5000),labels = seq(5000,250000,by = 5000), include.lowest = FALSE)
) %>% filter(marca %in% marcas.in)
#calculando as estatísticas por faixa
df.bars <- df.bars %>% group_by(km.fx,marca) %>% summarise(
n = n(),
ci.fipe = ci(preco.fipe),
media.fipe = mean(preco.fipe,na.rm = TRUE),
ci.anuncio = ci(preco),
media.anuncio = mean(preco,na.rm = TRUE)
)
df.bars <- df.bars %>% gather(stat,val,starts_with('ci'),starts_with('media'))
df.bars$tipo <- str_extract(df.bars$stat,'(?<=\\.).*$')
df.bars$stat <- str_extract(df.bars$stat,'^.*(?=\\.)')
df.bars <- df.bars %>% spread(stat,val)
df.bars$km.fx <- as.numeric(as.character(df.bars$km.fx))
df.bars <- df.bars %>% filter(km.fx <= 150000)
#gerando o gráfico
gg.post1 <- ggplot(df.bars %>% filter(tipo == "anuncio")) +
geom_line(aes(x=km.fx, y=media,colour=tipo,group=tipo),size = 1)+
geom_point(aes(x=km.fx, y=media,colour=tipo),size=0.8) +
geom_ribbon(aes(x=km.fx,ymin=media-ci,ymax=media+ci,fill=tipo,colour=tipo),alpha=0.4) +
facet_wrap(marca~.) +
labs(title = "Preço médio do carro por faixa de quilometragem",subtitle = "Marcas mais populares") + ylab("preço (R$)") + xlab("quilometragem") +
theme(axis.text.x = element_text(angle = 90, vjust=0.4,size=7),
axis.text.y = element_text(size=7),
strip.text.x = element_text(color='black',size=7))
gg.post1Para facilitar a comparação dos indicadores de depreciação de cada marca, abaixo mostramos esses indicadores na forma de uma tabela 1. Apenas mostraremos marcas que tem, pelo menos, 20 carros em cada faixa de quilometragem. No ranking abaixo vemos que Honda fica apenas em 6º lugar, já Toyota fica, de fato, no 1º lugar. Esse ranking é apenas preliminar, e além de estar fazendo algumas suposições (como linearidade da depreciação com relação à quilometragem, paridade entre os diferentes modelos de uma mesma marca, ausência de viés de seleção para marcas mais caras, entre outras), a amostra é pequena para algumas das marcas. Então deve ser utilizado com ressalva. Uma estratégia mais robusta talvez seja criar um indicador que não descarta um número tão grande de carros.
| Marca |
Preço Médio 10.000 km |
Preço Médio 150.000 km |
Indicador |
|---|---|---|---|
| Toyota | R$75.993 | R$55.210 | 73% |
| Hyundai | R$63.563 | R$37.349 | 59% |
| Nissan | R$63.264 | R$36.467 | 58% |
| Mitsubishi | R$93.648 | R$52.186 | 56% |
| Renault | R$52.084 | R$23.173 | 44% |
| Honda | R$75.735 | R$32.485 | 43% |
| Fiat | R$53.021 | R$22.615 | 43% |
| Ford | R$67.798 | R$28.502 | 42% |
| VW - VolksWagen | R$63.027 | R$24.165 | 38% |
| Peugeot | R$58.654 | R$21.401 | 36% |
| GM - Chevrolet | R$62.979 | R$22.587 | 36% |
Tabela com indicadores
Para criar a tabela com os indicadores de depreciação por marca, iremos utilizar o mesmo dataframe df.bars utilizado para criar o gráfico anterior. Do cálculo mostrado no código abaixo, fica claro porque a base de dados dos veívulos ficou tão reduzida para calcular os indicadores. O indicador considerado pode ser claramente melhorado. Um estimador mais robusta levaria em conta todos os veículos da base de dados. Quando fizer um novo post sobre o tema, discutirei alternativas mais interessantes para esse indicador.
#filtrando base para incluir apenas marcas com 20 imoveis e quilometragem máxima de 150.000
df.ind <- df.bars %>% filter(tipo == "anuncio",km.fx %in% c(10000,150000), n >= 20) %>% select(km.fx,marca,media)
df.ind <- df.ind %>% spread(km.fx,media)
df.ind$ind <- df.ind$`150000` / df.ind$`10000`
df.ind <- df.ind %>% arrange(desc(ind))
df.ind <- df.ind %>% drop_na()
df.ind <- df.ind %>% mutate_at(vars(`10000`,`150000`),list(~paste0("R\\$",format(.,digits = 0,big.mark = ".",decimal.mark = ",",scientific = FALSE))))
df.ind <- df.ind %>% mutate_at(vars(ind),list(~paste0(round(100*.,0),"%")))
#alterando nomes das variáveis na tabela
names(df.ind) <- c('Marca','Preço Médio<br>10.000 km','Preço Médio<br>150.000 km','Indicador')
#gerando a tabela
knitr::kable(df.ind,
align=rep('c', ncol(df.ind)),
escape = FALSE,
booktabs = TRUE,
caption = 'Índicador de depreciação do carro por marca.') %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"),full_width = F, position = "center") %>%
#column_spec(1, width = "60px") %>%
column_spec(4, background="darkorange", bold = T, color = "white") %>%
#row_spec(11, bold = T, color = "white", background = "darkorange") %>%
row_spec(1, bold = T) %>%
row_spec(6, bold = T)Conclusão
Sou um grande fã da banda Queen. Em 1976, ano que eu nasci, eles escreveram uma música chamada “Eu estou apaixonado pelo meu carro”. A música em si não é tão boa, mas me lembro que ao ouví-la me dei conta pela primeira vez da importância que um carro pode ter para uma pessoa. E quando estamos apaixonados, é difícil fazer avaliações racionais. Talvez essas pessoas sejam as mais beneficiadas por esse post, e pelo modelo sendo desenvolvido para refinar as estimativas de preço da FIPE.
Mesmo que para você o carro seja meramente um modo de locomoção, esse post pode ser útil. Com exceção de uma casa, o carro é geralmente o bem material mais caro que compramos ao longo da nossa vida. Ter uma estimativa mais precisa sobre o seu valor, bem como entender melhor como funciona a depreciação do mesmo, pode ajudar você, leitor, a economizar bastante dinheiro.