
App para ajustar as estimativas da tabela FIPE
By Neale Ahmed El-Dash on Oct 17, 2019
Nesse post discutiremos a dinâmica da desvalorização dos carros no mercado brasileiro, em função da idade e da quilometragem do veículo, apresentaremos um modelo estatístico que prevê o valor do carro ajustando o preço da tabela FIPE em função da quilometragem, e divulgaremos um app online que faz esse cálculo gratuitamente para qualquer carro com valor de mercado menor do que R$ 150.000, com idade de até 20 anos.
Introdução
A tabela FIPE, criada pela Fundação Instituto de Pesquisas Econômicas (FIPE) em 1973, é a principal referência de preço no mercado de carros seminovos e usados no país. Nesse post de algumas semanas atrás, discutimos com mais detalhes como as estimativas de preço dessa tabela são obtidas. Para a discussão neste post, basta entender que as estimativas da FIPE se baseiam apenas em Marca, Modelo, Ano e Tipo de combustível.
Ao comprar um carro em 2016, durante a negociação, senti muita falta de informação para poder ajustar os valores da tabela FIPE de acordo com a quilometragem do carro. Queria ter uma estimativa mais precisa do valor do carro que eu estava comprando. Depois dessa compra fiquei pensando sobre como poderiam ser ajustadas as estimativas da tabela FIPE, considerando outros fatores relevantes para determinar o preço. Minha solução foi baixar todas as ofertas de carros de um site especializado, adicionar a esses dados as estimativas de preço da tabela FIPE, e depois fazer um modelo onde o preço do carro depende não só do valor da tabela FIPE, mas também da quilometragem.
Nesse post discutirei como esse modelo foi construído, e também como utilizar o app online que torna os resultados do modelo acessíveis para qualquer pessoa1.
Os dados e o viés de seleção
Nessa iteração do modelo trabalhamos com os dados da tabela FIPE de Jun/2019 e com todos os carros anunciados no site Mercado Livre até o dia 10/09/2019, porém futuramente o modelo será atualizado mensalmente. Ao total foram considerados mais de 24 mil preços da FIPE e 150 mil anúncios de carros do Mercado Livre.
Antes de entrar em detalhes sobre o modelo que foi desenvolvido, mostraremos rapidamente como a idade e a quilometragem do carro afetam o preço do veículo. Na tabela 1 mostramos a depreciação por faixa de quilometragem com referência a primeira faixa de 10.000 quilometros. Nessa tabela é possível ver que a desvalorização do carro aumenta conforme aumenta a quilometragem do carro, e que essa depreciação têm um comportamento razoavelmente estável, sendo em média de R$ 2.500 para cada 10.000 km rodados. Também, após rodar 150.000 km, o carro perdeu, em média, 60% do seu valor.
|
Faixa de Km |
Preço Anúncio |
Depreciação |
Depreciação Acumulada |
Depreciação Percentual |
|---|---|---|---|---|
| 10000 | R$60.000 | R$ 0 | R$ 0 | 0.0 |
| 20000 | R$54.900 | R$5.100 | R$ 5.100 | 8.5 |
| 30000 | R$46.950 | R$7.950 | R$13.050 | 21.8 |
| 40000 | R$43.990 | R$2.960 | R$16.010 | 26.7 |
| 50000 | R$43.000 | R$ 990 | R$17.000 | 28.3 |
| 60000 | R$42.000 | R$1.000 | R$18.000 | 30.0 |
| 70000 | R$39.900 | R$2.100 | R$20.100 | 33.5 |
| 80000 | R$36.990 | R$2.910 | R$23.010 | 38.4 |
| 90000 | R$34.900 | R$2.090 | R$25.100 | 41.8 |
| 100000 | R$32.000 | R$2.900 | R$28.000 | 46.7 |
| 110000 | R$31.000 | R$1.000 | R$29.000 | 48.3 |
| 120000 | R$28.999 | R$2.001 | R$31.001 | 51.7 |
| 130000 | R$26.990 | R$2.009 | R$33.010 | 55.0 |
| 140000 | R$26.000 | R$ 990 | R$34.000 | 56.7 |
| 150000 | R$23.990 | R$2.010 | R$36.010 | 60.0 |
Dados dos anúncios
Como essa é uma análise preliminar dos dados dos anúncios, ainda não vou escrever sobre como esses dados foram extraídos da internet, nem sobre como as bases de dados de preços da tabela FIPE e dos carros anunciados no site Mercado Livre foram compatibilizadas. Por enquanto vou apenas disponibilizar a base de dados utilizada, a qual está no formato rds e pode ser baixada nesse link.
No bloco de código abaixo, mostro como criar a tabela resumo, por faixa de quilometragem.
dir = tempdir()
#código baixando os dados do site do PollingData
url <- "http://www.pollingdata.com.br/blog/desvalorizacao carro - 03-10-2019/df_post2.rds"
file.data = tempfile(tmpdir=dir, fileext=".rds")
download.file(url,file.data,method="curl")
df.post2 <- readRDS(file.data)
df.km <- df.post2 %>% group_by(km.fx.val) %>% summarise(
preco = median(preco,na.rm=TRUE)
) %>% filter(km.fx.val <= 150000)
df.km <- df.km %>% mutate(
depre = ifelse(is.na(lag(preco) - preco),0,lag(preco) - preco),
depre.tot = cumsum(depre),
depre.perc = round(100*(depre.tot / df.km$preco[1]),1)
)
df.km <- df.km %>% mutate_at(vars(-km.fx.val,-depre.perc),list(~paste0("R\\$",format(.,digits = 0,big.mark = ".",decimal.mark = ",",scientific = FALSE))))
names(df.km) <- c('Faixa de<br>Km','Preço<br>Anúncio','Depreciação','Depreciação<br>Acumulada','Depreciação<br>Percentual')
knitr::kable(df.km,
align=rep('c', ncol(df.km)),
escape = FALSE,
booktabs = TRUE,
caption = 'Depreciação do carro por faixa de Km.') %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"),full_width = F, position = "center")Na tabela 2, refizemos a tabela anterior, porém agora levando em consideração o ano do carro ao invês da quilometragem. Nesse caso, o comportamento da depreciação não é tão claro, principalmente nos anos de 2017 a 2019, destacados em laranja. Note como, em média, um carro de 2017 é mais caro do que um carro de 2018/2019. Claramente a realidade não é essa. Como o tamanho da amostra para esses anos mais recentes é bem grande, quase 10.000 veículos, a explicação mais provável é que exista algum tipo de viés nos dados dos carros mais novos.
|
Ano de Fabricação |
Preço Anúncio |
Preço FIPE |
Km | Depreciação |
|---|---|---|---|---|
| 2019 | R$43.990 | R$48.434 | 30280.5 | R$ 0 |
| 2018 | R$43.950 | R$44.445 | 32200.0 | R$ 40 |
| 2017 | R$53.994 | R$55.973 | 40000.0 | R$-10.044 |
| 2016 | R$49.900 | R$51.340 | 52000.0 | R$ 4.094 |
| 2015 | R$43.900 | R$44.917 | 64000.0 | R$ 6.000 |
| 2014 | R$39.900 | R$40.392 | 76003.0 | R$ 4.000 |
| 2013 | R$34.900 | R$34.746 | 84280.0 | R$ 5.000 |
| 2012 | R$32.000 | R$32.494 | 91283.0 | R$ 2.900 |
| 2011 | R$29.000 | R$29.388 | 100000.0 | R$ 3.000 |
| 2010 | R$25.899 | R$25.370 | 107000.0 | R$ 3.101 |
| 2009 | R$24.000 | R$24.521 | 114000.0 | R$ 1.899 |
| 2008 | R$21.900 | R$22.042 | 124626.0 | R$ 2.100 |
| 2007 | R$20.000 | R$21.032 | 130000.0 | R$ 1.900 |
| 2006 | R$18.890 | R$19.040 | 136000.0 | R$ 1.110 |
| 2005 | R$17.000 | R$17.411 | 142000.0 | R$ 1.890 |
| 2004 | R$15.900 | R$16.644 | 148000.0 | R$ 1.100 |
| 2003 | R$14.905 | R$14.781 | 151000.0 | R$ 995 |
| 2002 | R$12.800 | R$12.621 | 155724.0 | R$ 2.105 |
| 2001 | R$11.900 | R$11.793 | 150000.0 | R$ 900 |
| 2000 | R$11.900 | R$11.926 | 155828.0 | R$ 0 |
Tabela por ano
No bloco de código abaixo, mostro como criar a tabela resumo, por ano de fabricação dos veículos. Detalhes como a formatação dos números na tabela, e como destacar linhas de uma tabela estão disponíveis no código.
df.ano <- df.post2 %>% group_by(mod_ano) %>% summarise(
preco = median(preco,na.rm=TRUE),
preco.fipe = median(preco.fipe,na.rm=TRUE),
km = median(km,na.rm=TRUE)
) %>% filter(mod_ano >= 2000) %>% arrange(desc(mod_ano))
df.ano <- df.ano %>% mutate(
depre = ifelse(is.na(lag(preco) - preco),0,lag(preco) - preco),
depre.tot = cumsum(depre),
depre.perc = round(100*(depre.tot / df.ano$preco[1]),1)
)
df.ano <- df.ano %>% mutate_at(vars(-mod_ano,-depre.perc,-km),list(~paste0("R\\$",format(.,digits = 0,big.mark = ".",decimal.mark = ",",scientific = FALSE))))
names(df.ano) <- c('Ano de<br>Fabricação','Preço<br>Anúncio','Preço<br>FIPE','Km','Depreciação','Depreciação<br>Acumulada','Depreciação<br>Percentual')
df.ano <- df.ano[,1:5]
knitr::kable(df.ano,
align=rep('c', ncol(df.ano)),
escape = FALSE,
booktabs = TRUE,
caption = 'Depreciação do carro por idade.') %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"),full_width = F, position = "center") %>%
row_spec(1, bold = T, color = "white", background = "darkorange") %>%
row_spec(2, bold = T, color = "white", background = "darkorange") %>%
row_spec(3, bold = T, color = "white", background = "darkorange")Para entender qual tipo de viés pode estar afetando os dados, é importante pensar mais detalhadamente sobre como os dados dos anúncios dos veículos foram obtidos, e como estão sendo utilizados. Na base de dados sendo analisada estão todos os valores de veículos anúnciados no site Mercado Livre até o dia 10/09/2019. Dessa forma, nossa base de dados se refere ao mercado de veículos semi-novos e usados, porém estamos usando esses dados para estimar os preços de qualquer veículo usado do país, mesmo aqueles que não foram colocados a venda (anunciados). Ou seja, estamos utilizando os carros anunciados no site Mercado Livre como uma amostra da população de todos os carros usados do país.
Se tempo e dinheiro não fossem problemas, e fosse possível obter uma listagem com todos os carros do país (por exemplo a lista com todos os IPVA’s), poderíamos realizar essa pesquisa da maneira ideal, como aprendemos nos livros de amostragem no curso de estatística. A estratégia mais simples seria utilizar a listagem de toda a população de carros do país para selecionar uma amostra aleatória simples, de forma que todos os carros tivessem a mesma chance de participar da pesquisa. Uma amostra aleatória simples consiste em associar uma probabilidade de seleção uniforme para cada carro, e através de algum mecanismo aleatório determinar quais carros pertencerão à pesquisa.
Entretando, muitas vezes não é possível selecionar uma amostra conforme descrito acima, utilizando um mecanismo aleatório. Quando isso não ocorre, é possível que as unidades amostrais tenham algum viés sistemático pois o pesquisador não consegue controlar quem participará da pesquisa. Esse viés pode, em menor ou maior grau, fazer com que as unidades amostradas sejam diferentes das outras unidades populacionais que não estão na amostra. Esse tipo de viés é denominado de viés de seleção.
O exemplo real desse viés que eu mais gosto ocorreu durante a Segunda Guerra Mundial. O Governo Britânico pediu ao estatístico Abraham Wald para ajudá-lo a decidir quais partes dos aviões de guerra deveriam ser reforçadas com armadura. Após analisar os dados, ele recomendou que as partes que não estavam danificadas fossem reforçadas! Inicialmente essa recomendação parece invertida, porém Wald percebeu que os dados que ele analisou vieram apenas dos aviões que sobreviveram. Ou seja, os Britânicos somente tinham dados dos aviões que conseguiram voltar a Inglaterra. Aqueles que foram derrubados em território inimigo não estavam na amostra. Pensando assim, os danos dos aviões na amostra mostravam na verdade os locais onde um avião podia ser danificado e ainda assim voltar para casa.
A suposição básica de Wald nessa análise era de que a localização dos tiros nos aviões eram aleatórias, e que os inimigos não conseguiam mirar em partes especifícias dos aviões. Nesse caso todas as partes dos aviões deveriam estar igualmente danificadas se não fosse pelo viés de seleção. Ou seja, as partes dos aviões na amostra que não tinham danos eram tão importantes que quando eram danificadas causavam a queda do avião.
No nosso caso dos anúncios de carros, minha intuição é que existe algum viés de seleção na escolha de quais carros com 3 anos ou menos são anunciados, e isso faz com que, sistematicamente, carros com preço mais baixo sejam colocados a venda. Para entender se existe algum tipo de diferença sistemática nesses veículos, vamos analisar mais detalhadamente a tabela 2. A primeira coisa que chama a atenção é que os carros de 2019 têm uma quilometragem bem alta, de mais de 30.000 km. Considerando que a média anual é de 12.000 km, e que o ano de 2019 ainda não terminou, esse valor é quase o triplo do que deveria ser. Ou seja, parece existir um viés de seleção que faz com que carros de 2018 e 2019 anunciados tenham uma quilometragem maior.
Porém se a única consequência desse viés fosse a alta quilometragem, os preços da tabela FIPE não estariam enviesados, visto que eles não dependem da quilometragem. Olhando a tabela 2, percebemos que a diferença entre os preços da tabela FIPE de 2018/2019 e 2017 também mostram esse viés. Ou seja, parece que o viés também tem a ver com as marcas (e modelos) que são anunciadas. Pensando nisso, agrupei as marcas em 5 classes, sendo que as marcas mais caras foram classificadas como classe A, e as mais baratas como Classe E. Na figura 1 abaixo, é possivel ver o percentual de cada classe para cada ano de fabricação. Claramente nos anos de 2017 a 2019 esses percentuais são bem diferentes. Em 2019, por exemplo, 50% dos carros são da classe D, em nenhum outro ano esse percentual é maior do que 21%. Já em 2018, 45% dos carros são da classe C, em nenhum outro ano antes de 2017 esse percentual é maior do que 28%.

Figure 1: Diferença de perfil dos carros na amostra
Classe das marcas
Os agrupamentos das diferentes marcas de veículos poderiam ser criados de muitas formas diferentes. O ponto principal era que, de alguma forma, dependessem do preço médio ou mediano do veículo. No bloco de código abaixo mostro como as faixas utilizadas nesse post foram criadas.
A escolha de quais cortes de preço médio utilizar foi subjetiva, porém baseada em dois critérios principais: queria faixas com um número razoável de marcas e também que representassem um percentual mínimo aceitável de carros anunciados.
O dataframe df.peso criado abaixo será utilizado no próximo bloco de código, para gerar os pesos de ajuste do viés de seleção.
df.cortes <- df.post2 %>% filter(mod_ano >=2010) %>% group_by(marca) %>% summarise(
n = n(),
preco.medio = mean(preco),
preco.med = quantile(preco,probs = 0.5)
)
df.cortes <- df.cortes %>% arrange(desc(preco.med))
df.cortes <- df.cortes %>% mutate(
acum = round(100*cumsum(n) / sum(n),1),
classe = case_when(
preco.med >= 60000 ~ "Classe A",
preco.med >= 43000 ~ "Classe B",
preco.med >= 39000 ~ "Classe C",
preco.med >= 35000 ~ "Classe D",
TRUE ~ "Classe E"
)
)
df.cortes <- df.cortes %>% select(marca,classe)
df.classe <- df.post2 %>% left_join(df.cortes)
df.classe <- df.classe %>% filter(mod_ano >= 2010) %>% drop_na()
df.classe <- df.classe %>% group_by(mod_ano,classe) %>% count()
df.peso <- df.classe
df.classe <- df.classe %>% group_by(mod_ano) %>% mutate(
n = n / sum(n)
)# %>% spread(mod_ano,n)
gc <- ggplot(data=df.classe,aes(x=mod_ano,y=n,fill = classe,label=round(100*n,0))) + geom_bar(stat = "identity")
gc <- gc + geom_text(size = 3, position = position_stack(vjust = 0.5))
gc <- gc + labs(title = "Distribuição de classes de marca",subtitle = "De 2010 a 2019") +
ylab("Percentual (%)") + xlab("Ano de Fabricação")
gcTentar dizer qual é a causa do viés de seleção sem mais informações é muito difícil, mas meu instinto me diz que deve ser uma combinação de dois fatores: algumas empresas podem trocar as frotas de veículos depois de 2 ou 3 anos e algumas pessoas compram e rodam muito no primeiro ano, para depois trocar de carro.
Mesmo sem saber qual é a causa real do viés de seleção, é possível ajustar a base de dados para tentar atenuar esses efeitos. Uma estratégia bastante comum, a qual vou adotar aqui, é denominada de ponderação (ou pós-estratificação) da base de dados. Isso envolve dar pesos diferentes para as observações do banco de dados. Para fazer inferências a partir de uma base de dados ponderada, é necessário incluir os pesos na estratégia de estimação. Especificamente nesse caso, a ponderação utilizada consiste em dar uma peso menor para classes de marcas que estão super-representadas nos três primeiros anos, e um peso maior para as classes sub-representadas. Como referência para determinar qual deve ser o tamanho relativo de cada classe de marca foram utilizados os anos de 2014 a 2016. Na figura 2 mostramos como ficou o percentual ponderado de cada classe para cada ano de fabricação.
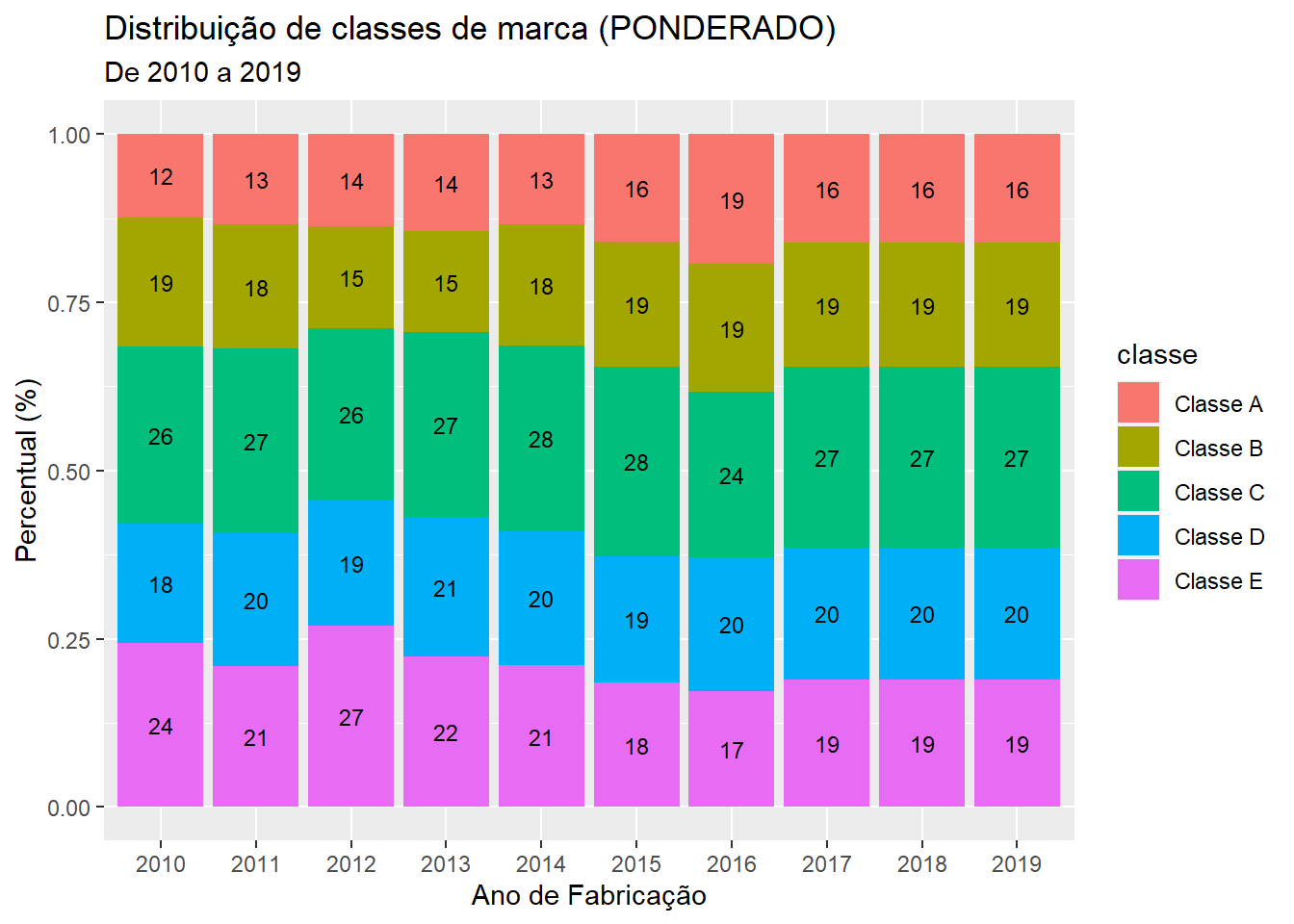
Figure 2: Diferença de perfil dos carros na amostra após ponderação
Ajuste do viés
No dataframe df.peso os pesos para os anos de 2017 a 2019 são criados. Para todos os outros anos o peso será de 1. Note que como utilizei apenas uma variável de ponderação, não foi necessário recorrer a algoritmos mais complexos de ponderação. O peso de cada classe de marca é definido como sendo pesoclasse k=perc.referênciaclasse kperc.anoclasse k.
df.peso <- df.peso %>% filter(mod_ano %in% 2014:2016) %>% group_by(classe) %>% summarise(
univ = sum(n)
)
df.peso <- df.peso %>% ungroup() %>% mutate(
univ = univ / sum(univ)
)
df.peso <- df.classe %>% left_join(df.peso) %>% filter(mod_ano %in% 2017:2019)
df.peso$peso <- df.peso$univ / df.peso$n
df.peso <- df.peso %>% select(mod_ano,classe,peso)
df.post2 <- df.post2 %>% left_join(df.cortes) %>% left_join(df.peso)
df.post2$peso <- ifelse(is.na(df.post2$peso),1,df.post2$peso)
df.classe2 <- df.post2 %>% filter(mod_ano >= 2010) %>% drop_na()
df.classe2 <- df.classe2 %>% group_by(mod_ano,classe) %>% summarise(
n = sum(peso)
)
df.classe2 <- df.classe2 %>% group_by(mod_ano) %>% mutate(
n = n / sum(n)
)# %>% spread(mod_ano,n)
gc2 <- ggplot(data=df.classe2,aes(x=mod_ano,y=n,fill = classe,label=round(100*n,0))) + geom_bar(stat = "identity")
gc2 <- gc2 + geom_text(size = 3, position = position_stack(vjust = 0.5))
gc2 <- gc2 + labs(title = "Distribuição de classes de marca (PONDERADO)",subtitle = "De 2010 a 2019") +
ylab("Percentual (%)") + xlab("Ano de Fabricação")
gc2A estratégia adotada ajuda com a correção do viés, mas ainda pode ser melhorada. Neste post utilizamos esta estratégia baseada nas classes de marcas, porém na próxima iteração do modelo estatístico, ponderar os dados com relação aos modelos dos carros pode apresentar melhores resultados do que apenas ponderar por marcas.
O modelo de ajuste da tabela FIPE
A objetivo do modelo apresentado nessa seção é explicar a diferença entre os preços da tabela FIPE e os preços praticados nos anúncios de venda de veículos. A diferença pode ser explicada por vários fatores, como quilometragem, estado de origem, opcionais e lataria, bem como se teve apenas um dono, se é financiado, se a documentação está regularizada, e se a revisão foi feita na concessionária, entre outras. No modelo utilizado aqui, entretanto, utilizamos apenas quilometragem para explicar a diferença.
A ideia é criar um fator de ajuste baseado na tabela FIPE, mas que de fato forneça ao usuário uma estimativa do preço de mercado, algo mais útil ao leitor na hora de negociar o preço de um carro do que o valor da tabela FIPE.
Para treinar o modelo foram utilizados os dados descritos acima, juntamente com os pesos calculados de forma a reduzir o impacto do viés de seleção. Nesse modelo utilizamos diferentes codificações da variável de quilometragem, com o objetivo de permitir mais flexibilidade na relação entre preço e quilometragem.
Utilizamos um tipo de modelo muito interessante, conhecido como modelo multinível de efeitos mistos, o qual permite que cada marca/modelo de carro tenha a sua própria relação entre quilometragem e preços. Nos casos de modelos de carros onde a amostra é muito pequena (ou inexistente), é utilizado como referência a marca do carro (um nível hierárquico acima). Ou seja, mesmo em casos específicos com poucos casos, ainda é possível obter uma estimativa razoável.
O modelo foi planejado de forma a impedir que estimativas de preço negativas sejam possíveis, porém algumas incoerências ainda são possíveis. Como não estamos impondo uma relação estritamente descrescente entre quilometragem e preço, é possível que em alguns casos as estimativas mostrem aumento de preço quando a quilometragem aumenta. Esses casos devem ser desconsiderados pelo usuário.
Diferentemente do que tenho feito em outros posts, dessa vez não divulgarei detalhes, nem o código do modelo, pois espero que ele possa ser monetizado no futuro. Apenas mostrarei, de forma superficial, a fórmula utilizada pelo modelo:
log(preço.anunciopreço.fipe) =1+km + f(km)+(1+km |marcas.carro)+(1+km |modelos.carro),
onde os símbolos (.|grupo) representam efeitos aleatórios para a variável de agrupamento, indicando que para cada categoria dessa variável discreta pode haver uma relação linear diferente entre preço e quilometragem. Já o símbolo f(km) indica que diferentes formas funcionais da quilometragem podem ser inseridas no modelo, como √km ou km2.
O app online
O app com o modelo pode ser acessado nesse link ou nessa seção do post. Os resultados desse modelo de ajuste da tabela FIPE foram disponibilizados para qualquer pessoa poder acessar e calcular suas estimativas. Não é obrigatório, porém deixo a opção do usuário cadastrar seu email e senha, porque gostaria de ter uma ideia de quantas pessoas usaram o app. Para acessá-lo basta clicar no botão “log in”, não é necessário preencher nenhum dos dois campos.
O uso do app é simples; basta escolher a marca, o modelo, o ano de fabricação e o tipo de combustível e preencher a quilometragem do carro de interesse. Feito isto, basta clicar no botão “Gerar Estimativa”. O resultado do modelo será um gráfico mostrando como o preço de mercado do veículo descresce de acordo com o aumento da quilometragem. Além disso, destacado em vermelho encontra-se o preço da tabela FIPE, e destacado em azul o preço de mercado (FIPE ajustada).
Conclusão
O modelo de ajuste da tabela FIPE já estava pronto quando descobri o viés de seleção dos carros com menos de 3 anos de idade. Para esse tipo de análise, como para qualquer trabalho estatístico, a análise descritiva dos dados é essencial. Quanto mais você brincar com os dados, mais familiarizado ficará com o problema, e mais fácil será melhorar o modelo.
Um dos motivos que me levou a desenvolver o app foi para que eu pudesse, visualmente, analisar diferentes modelos de carro, para ver se os resultados individuais faziam sentido. Em inglês chamamos isso de “sanity check”, ou seja, fazer um teste de sanidade dos resultados individuais. Essa possibilidade de visualizar interativamente os dados é fantástica, e nesse caso onde temos mais de 24 mil modelos de carros sendo ajustados, permite que o analista tenha um feeling muito melhor sobre o que está acontecendo com modelo. Testei o modelo utilizando muitos carros conhecidos: o meu, os dos meus pais, e os de amigos. Dessa forma os resultados do modelo ficaram mais tangíveis, me ajudando a encontrar possíveis melhorias.
Mesmo fazendo vários testes, e olhando dezenas de estimativas individuaís como descrito acima, existirão estimativas individuais que não farão sentido. Por isso é importante continuar desenvolvendo o modelo, aumentando a base de dados, e estudando como funcionam os preços de anuncíos de carros.
Quando terminei o meu mestrado fui trabalhar no “mercado”, como dizem, eu tive muita dificuldade no começo dessa nova etapa de vida. Naquela época eu acreditava que existia uma única forma correta, ideal, de fazer as análises estatísticas. Eu achava que as outras opções não eram aceitáveis. A dificuldade principal era que eu nunca sabia qual era “A” melhor forma possível de resolver o problema, sem falar que muitas vezes não tinha acesso a um software que tivesse a rotina computacional necessária para fazer essa análise. Com o passar do tempo, percebi que, em primeiro lugar, raramente existe uma única forma correta de resolver um problema, e em segundo lugar, que era melhor uma solução aceitável encontrada dentro das janelas de tempo e recursos disponíveis, do que uma solução ótima que não ficasse pronta no prazo. Depois, quando houver mais tempo, você pode sempre melhorar aquela solução inicial. Kim Collins, um atleta profissional de São Cristovão e Nevis, que chegou a ser campeão mundial dos 100 metros, resumiu bem essa ideia quando disse:
“Esforce-se para ter melhorias constantes ao invês de perfeição.”
Ao disponibilizar os resultados de um modelo estatístico dessa forma, permitimos que o leitor gere estimativas levando em conta o seu perfil (ou nesse caso, o perfil do seu carro). Se todos os modelos fossem disponibilizados dessa forma, resolveríamos a questão discutida nesse post, sobre a impossibilidade de pessoas obterem estimativas baseadas no seu perfil ao invês de baseadas no perfil médio da população.↩︎