Introdução

É cada vez mais comum encontrar notícias na mídia sobre alimentação saudável. Muitas vezes essas notícias focam no valor nutricional dos alimentos, na quantidade de gordura ou na opinião de nutricionistas. Entretanto tem se tornado cada vez mais comum encontrar notícias que destacam os riscos de desenvolver câncer associado ao consumo de certos tipos de alimentos. Um busca rápida na internet aponta risco no consumo de carnes vermelhas, alimentos ultra-processados e bebidas alcoólicas.

São tantas notícias, sobre uma variedade tão grande de alimentos que fazem parte da rotina dos brasileiros, que pode ser difícil entender o que significam essas notícias. O que fazer, especialmente quando se trata de algo que pode ser muito prazeiroso como comida. Uma das primeiras preocupações hoje em dia, com tantas notícias falsas, seria, antes de tudo, verificar se a notícia é real. Veja se outros veículos de mídia divulgaram informações similares. Se não encontrar, ignore essa notícia. Só considere deixar de fazer algo que você gosta se houverem evidências claras que faz mal a sua saúde.

Além disso, muitas notícias sobre saúde, apesar de não serem falsas, são superficiais. Reproduzem conteúdo de algum outro site, ou então de alguma pesquisa científica, porém não se dão ao trabalho nem de informar a fonte original da informação. Querem gerar clicks apenas, não informar a população sobre riscos reais. Meu conselho: ignore-as também. Não perca seu tempo com notícias superficiais. A fonte da pesquisa ou da informação é essencial, é como se fosse um selo de qualidade. Se você pretende utilizar esse conhecimento para de fato modificar a sua vida, seja seletivo. Se a fonte original não está na notícia, existe uma grande chance de que o autor não leu a pesquisa original, muito menos se preocupou em checar os dados. É como aquela brincadeira de telefone sem fio, a chance de você estar recebendo informações parciais ou distorcidas é enorme. Não abra mão de algo importante pra você sem necessidade.

Se você restringiu sua atenção a reportagens respeitando os filtros que descrevi acima, a informação que você recebeu tem potêncial para ser confiável. Meu objetivo nesse post é discutir como interpretar essas estatísticas de forma que elas possam ser úteis para você. Que ajudem VOCÊ a decidir como levar a SUA vida.

Incidência e Risco Relativo

Para conseguir avaliar corretamente a chance de desenvolver câncer que você corre ao consumir um dado alimento, você depende de três informações fundamentais. Abaixo vou discutir essas informações. Para todas as definições de termos estatísticos, estou utilizando como referência um dicionário estatístico (Everitt 2006).

1. Contexto: Isso se refere à quantidade do alimento consumido e o tempo de consumo desse alimento. Todas as evidências publicadas por um estudo são referentes a esse contexto.
   
2. Incidência: Se refere à taxa com que pessoas sem uma doença desenvolvem essa doença durante um período específico de tempo. Usualmente ela é apresentada como sendo um percentual.
   • Ela é calculada como segue: \[Incidência = \frac{número\ de\ casos\ novos\ de\ uma\ doença\ num\ certo\ período\ de\ tempo}{população\ em\ risco\ de\ desenvolver\ a\ doença\ neste\ período\ de\ tempo}.\]
     
3. Risco Relativo: É uma medida da associação entre exposição a um fator e o risco de ocorrência de um certo resultado. Assim um risco relativo de 5, por exemplo, quer dizer que uma pessoa exposta ao fator tem 5 vezes mais chance de desenvolver a doença do que alguém não exposto.
   • Ele é calculado como segue: \[Risco\ Relativo = \frac{incidência\ de\ pessoas\ expostas\ ao\ fator}{incidência\ de\ pessoas\ não\ expostas\ ao\ fator}.\]

O contexto de um estudo inclui qual é a quantidade de alimento consumido e o período de tempo pelo qual esse alimento foi consumido. Esses compõem o fator de risco ao avaliar o risco de câncer causado pelo consumo de algum alimento.

A incidência é uma das informações mais importantes se você quiser avaliar o seu risco. Ela é uma probabilidade, que é uma idea difícil de ser compreendida por muitas pessoas. Num livro muito legal sobre o ensino de probabilidade (Gage and Spiegelhalter 2016), os autores sugerem que a forma mais intuitiva de interpretar uma probabilidade corretamente não é utilizando percentuais, mas uma outra representação, chamada de “frequência esperada”. Ao invês de dizer “A probabilidade de X é de 30%”, dizemos que “em 100 situações como essa, nos esperamos que X ocorra 30 vezes”.

Apesar de ser muito simples, essa forma de falar sobre probabilidades resolve um problema de interpretação muito importante (conhecido como “classe de referência”). Pense sobre a frase “A probabilidade de chover amanhã é de 30%.” O que quer dizer? Que vai chover 30% do tempo? Que vai chover em 30% da área? Na realidade quer dizer que em 100 previsões feitas pelo computador em situações como esta, observa-se chuva em 30 delas. Usando a frequência esperada, a referência é explicita, eliminando a ambiguidade.

Como exemplo, imagine que a incidência de um tipo específico de câncer seja de 0,5% em pessoas que comem 50g por dia de bacon, durante um ano. A situação corresponde a uma em cada 200 pessoas com essa alimentação desenvolver tal câncer. Para encontrar a base de 200 pessoas, a conta é simples. Basta dividir 1 pela probabilidade de interesse; no caso temos que \(\frac{1}{0.005}=200\) pessoas. Para visualizar quanto isso representa, veja a figura 1.

Figure 1: Incidência de câncer em pessoas que consomem 50g de bacon por dia, durante um ano

require(tidyverse)
library(waffle)
library(extrafont)

dir <- 'dir.local.fontes'
extrafont::font_import(path=dir, pattern = "awesome", prompt = FALSE)
loadfonts(device = "win")

cancer <- c(`Saudável`=199, `Câncer`=1)
#waffle(cancer, rows=10, use_glyph = "male", glyph_size = 6,size=0.1, colors=c("blue","red"),legend_pos = "bottom")
waffle(cancer, rows=10, glyph_size = 6,size=0.1, colors=c("blue","red"),legend_pos = "bottom")

Algumas vezes nem no próprio artigo científico original divulga claramente a incidência. Isso ocorre porque é muito comum utilizar, em estudos médicos, um tipo de modelo¹ estatístico conhecido como modelo de riscos proporcionais de Cox². Esse tipo de modelo é utilizado essencialmente pra entender o impacto relativo de diversos fatores no risco de desenvolver alguma doença. Como é relativo, não é necessário explicitamente saber a incidência. Porém, geralmente, “escondido” em algum lugar do texto, é possível extrair essa informação.

No contexto discutido aqui, o risco relativo mede o quanto é, em média, a propensão de uma pessoa desenvolver uma doença se consumir um tipo de alimento. É importante perceber que essa é uma medida relativa, não absoluta. Então quando o autor fala em risco 10% maior de câncer ao consumir algum tipo de alimento, quer dizer que a incidência do câncer em quem consome esse alimento é 10% maior do que em quem não consome esse alimento. O risco relativo então é de 1,1. Apesar de saber que há um aumento, sem conhecer as incidências em si, é dificil avaliar de forma objetiva qual é a chance real de desenvolver o câncer. Um aumento de 10% de uma incidência muito baixa continua sendo baixa.

Voltando ao exemplo do câncer acima, imagine que a incidência de um tipo específico de câncer seja de 0,2% em pessoas que consomem menos de 50g de bacon por dia, durante um ano. Nesse caso, a frequência esperada é de que uma em cada 500 pessoas³ tenha esse tipo de câncer. Ou seja, nesse exemplo, o risco relativo desse tipo de câncer para quem consome 50g de bacon por dia, durante um ano, é 2,5 vezes maior se comparado com quem consome menos de 50g. Esse valor pode ser calculado usando tanto a incidência (\(\frac{0,5\%}{0,2\%}=2,5\)) quanto a frequência esperada (\(\frac{500}{200}=2,5\)).

Entender o risco relativo também pode ser facilitado pelo uso da frequência esperada. O segredo é comparar as duas incidências utilizando o mesmo denominador⁴. O denominador a ser escolhido tem que permitir que a frequência esperada seja um número inteiro (de pessoas), tanto para quem está no fator de risco, quanto para quem não está. Nesse caso, o denominador é 1000, que é o mínimo múltiplo comum⁵ (MMC) entre as frequências esperadas de 200 e de 500. Colocando as duas incidências com o mesmo denominador, é fácil ver que a incidência de câncer em quem consome 50g de bacon é de 5 em cada 1000, e para quem consome menos de 50g é de 2 em 1000. Ou seja, 3 pessoas a mais em cada 1000. Para visualizar o quanto isso representa, veja a figura 2. Os ícones vermelhos de pessoas representam quantos casos a mais de câncer ocorrerão por comer 50g ou mais de bacon por dia, por um ano.

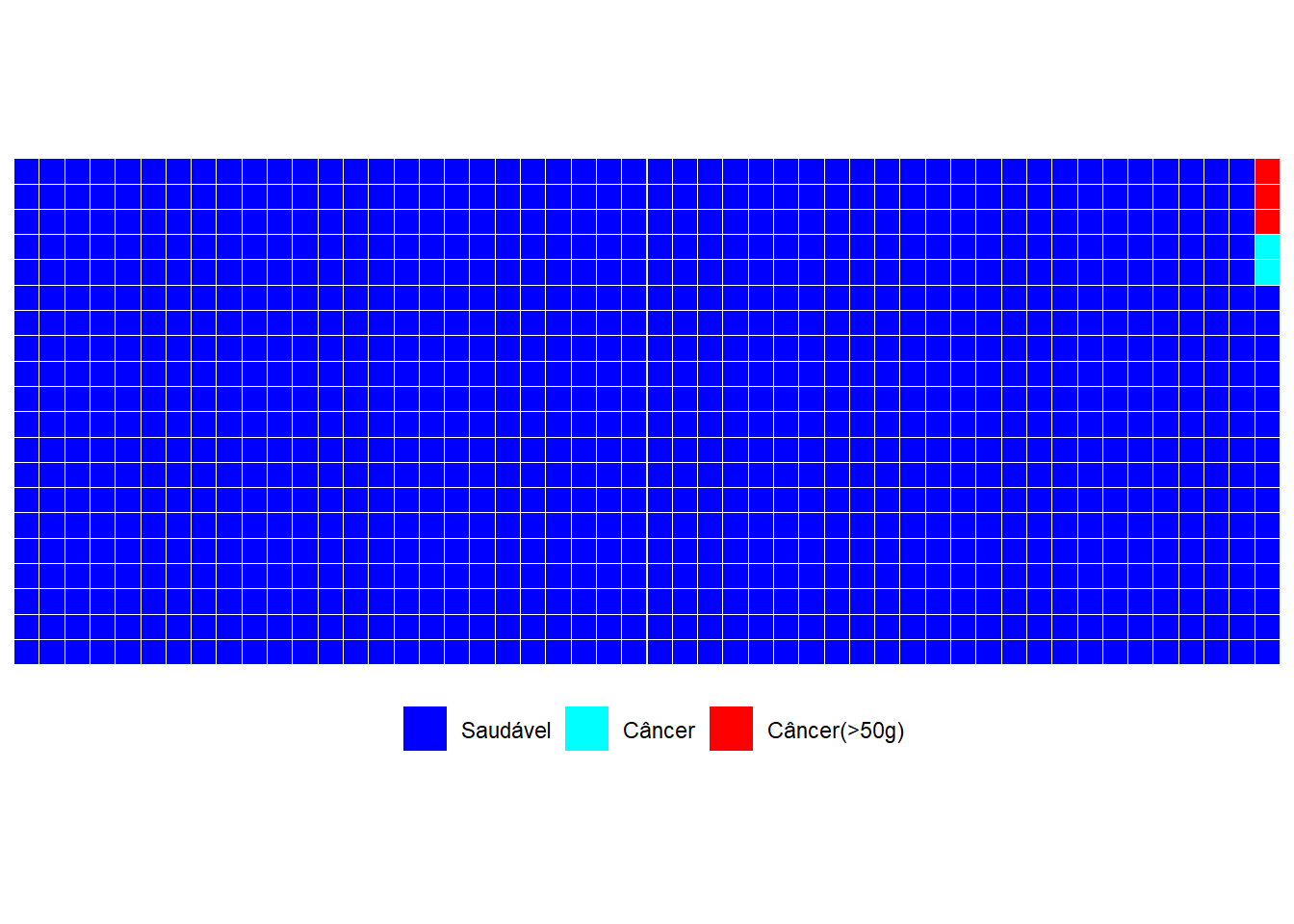
Figure 2: Aumento do risco relativo de câncer em pessoas que consomem mais de 50g de bacon por dia, durante um ano

cancer <- c(`Saudável`=995, `Câncer`=2, `Câncer(>50g)`=3)
#waffle(cancer, rows=20, use_glyph = "male", glyph_size = 5,size=0.1, colors=c("blue","cyan","red"),legend_pos = "bottom")

waffle(cancer, rows=20, glyph_size = 5,size=0.1, colors=c("blue","cyan","red"),legend_pos = "bottom")

Exemplo de reportagem

Nesta seção vamos ver como se aplicam os conceitos aprendidos na seção anterior. Utilizaremos a seguinte reportagem como referência. Nela, o autor diz que o consumo de alimentos ultraprocessados aumenta o risco de câncer. Alimentos ultraprocessados são alimentos industrializados e prontos para consumo, como biscoitos doces e salgados, refrigerantes, refrescos, salgadinhos, cereais matinais, embutidos, pratos congelados entre outros.

Se você buscar o termo “comida ultraprocessada risco cancer” no google, encontrará diversas reportagens sobre o mesmo tema, de outlets respeitáveis como o jornal Estadão, a revista Galileo Galilei, a USP e a BBC, entre outros. Dificilmente uma notícia falsa estaria em tantas fontes confiáveis. Além disso, no primeiro parágrafo a reportagem já faz menção ao estudo científico. Ou seja, essa notícia passa em todos os filtros de qualidade mencionados no começo do post.

O parágrafo a seguir é o único da reportagem que faz menção aos resultados do estudo:

“Com esses dados em mãos, eles descobriram que, para cada aumento de 10% na proporção de comida ultraprocessada consumida, o risco de encarar um tumor subia 12%. A probabilidade de ter especificamente o câncer de mama ficava 11% maior. O dado assusta mais ainda se considerarmos que, em vários países, esse tipo de produto representa entre 25 e 50% do total de calorias ingeridas em um dia.”

Ao ler esse parágrafo, o leitor pode ficar preocupado. Mas antes de ficar chocado com essa estatística de 12% de aumento do risco de câncer, pense sobre o três itens descritos anteriormente: 1) Contexto, 2) Incidência e 3) Risco relativo. Nesse reportagem falta especificar o contexto e a incidência. Sem eles, é impossível avaliar a chance real de desenvolver câncer. Para fazer isso, ou o leitor tem que buscar outra fonte de informação, ou acessar o link do estudo original.

Acessando o artigo original, é possível entender o contexto do estudo, embora seja relativamente complexo. Adultos voluntariaram para participar do estudo, que foi realizado por 9 anos, entre os 2009 e 2017, na França. Os participantes preencheram questionários sobre saúde e outras variáveis relevantes, além de um questionário sobre o que eles comeram nas últimas 24 horas. O questionário sobre alimentação foi repetido a cada 6 meses. Na análise dos resultados foram consideradas as 104.980 pessoas que preencheram pelo menos 2 questionários sobre sua alimentação. A dieta dos respondentes foi categorizada de acordo com a proporção que os alimentos ultraprocessados representavam do total de alimentos ingeridos.

Com essas informações, já é possível entender melhor a que o parágrafo destacado da reportagem se refere quando diz “para cada aumento de 10% na proporção de comida ultraprocessada consumida”. Se do total de comida que você consome, você aumentar a proporção de alimentos ultraprocessados em 10%, o risco relativo de câncer aumenta em 12%. Note que, nesse caso, o referencial é a própria pessoa, e a quantidade de tempo do estudo não é relevante. Isso só é possível porque no estudo estão utilizando o modelo de riscos proporcionais de Cox mencionado acima. Utilizar modelos complexos permite o uso de referenciais mais interessantes. Porém, ao fazer isso, mais suposições sobre o processo de desenvolvimento de câncer têm que ser feitas. É uma troca: simplificamos nossa visão do mundo para facilitar a compreensão do processo.

Na conclusão do artigo, é possível encontrar a incidência de câncer, que nesse caso é de 0,786%. Assim, a incidência para quem aumenta a ingestão de alimentos ultraprocessados na sua dieta em 10% é, em média, de 0,88%. Iremos arredondar essas incidências para uma casa decimal para facilitar as contas, e também porque estatísticas não são tão precisas. Assim temos que 8 em cada 1.000 pessoas desenvolvem câncer no período de um ano (na França). Se todas as pessoas aumentassem seu consumo de alimentos ultaprocessados em 10%, teríamos então 9 pessoas em cada 1.000 desenvolvendo câncer. Ou seja, um acréscimo de 1 pessoa por 1.000 habitantes, para cada aumento de 10% de alimentos ultraprocessados, por ano. A figura abaixo ajuda a visualizar o quanto isso representa.

Figure 3: Aumento do risco relativo de câncer em pessoas que aumentam em 10% o consumo de alimentos ultraprocessados (AU)

Uma pergunta natural é: quão confiável são as estimativas desse modelo? Além da questão do erro amostral (veja o post se tiver interesse no assunto), todo modelo faz suposições. O modelo desse artigo não é diferente. O grau de complexidade do tema é enorme, não há como realizar um estudo desse porte sem fazer muitas suposições. Mas talvez a suposição mais importante seja sobre a linearidade do aumento da chance de desenvolver câncer com relação ao consumo de alimentos ultraprocessados. Será que é realista supor que uma pessoa que aumenta a ingestão de ultraprocessados de 0% para 10% da sua dieta, aumentará a chance de ter câncer da mesma forma que uma pessoa que passa de 70% para 80%? Em ambos os casos o aumento foi de 10%, porém esses exemplos estão em lados opostos da escala no que se refere a alimentação saudável.

Além disso, o modelo só pode levar em conta as variáveis endógenas, ou seja, aquelas que estão contidas nos questionários que foram preenchidos pelos respondentes. As variáveis utilizadas nesse modelo foram: idade, sexo, índice de massa corporal, altura, atividade física, status de fumante, consumo de álcool, consumo de calorias, histórico familiar de câncer e nível educacional. Essas variáveis são utilizadas pelo modelo para ajustar as estimativas, pois elas também explicam a incidência de câncer. Porém claramente existem muitas outras variáveis exógenas que podem ser extremamente relevantes, como modo de vida, exposição a poluentes, stress, entre outras. E essas variáveis não podem ser incluídas no modelo.

Existe também a questão de quais alimentos são classificados na categoria de alimentos ultraprocessados. Será que um pão integral industrializado é tão diferente de um pão integral caseiro? Provavelmente existe uma diferença bem grande no potencial de causar câncer dos diferentes alimentos pertencentes a esse grupo.

Uma outra ressalva é que a dieta dos franceses pode ser muito diferente da dos brasileiros. Até mesmo com relação a quais alimentos ultraprocessados são consumidos. E essas diferenças podem fazer com que o modelo não seja facilmente generalizável para outros países.

Eu gosto de usar citações quando escrevo. Me ajudam a passar conceitos importantes. Sem dúvida a citação que eu mais utilizo é essa: “Todos os modelos estão errados, mas alguns são úteis”, do estatístico George Box. Ela é muito apropriada nesse caso. Apesar desse modelo estar errado, ele pode ser útil. O modelo acima prevê 1 pessoa em cada 1.000 desenvolvendo câncer por ano em média, se toda a população aumentar seu consumo de alimentos ultraprocessados em 10%. Se pensarmos na França toda, que tem 55 milhões de adultos, representa 55.000 novos casos de câncer por ano. Para pensar em políticas públicas, esse modelo pode ser bastante útil. Nesse contexto não há necessidade das estimativas serem tão precisas.

Porém para ser utilizado por você, leitor, para tentar inferir a sua chance de desenvolver câncer ao se alimentar de alimentos ultraprocessados, o modelo provavelmente erra muito. Não é possível nem avaliar o impacto das variáveis endógenas na sua chance de desenvolver câncer, pois esses resultados não estão disponíveis de forma acessível. Ou seja, você não conseguirá incluir as suas informações pessoais para obter uma estimativa que reflita o seu perfil. Por todos esses motivos, não exagere a importância nem a precisão dessas estimativas.

Essa distinção entre o uso de estatísiticas para o coletivo ou para o individual é importante. Ela também está relacionada a outra questão sobre a qual tenho refletido muito: será que a estatística é preconceituosa? Mas isso é material para um outro post.

Conclusão

Espero que o leitor não se sinta decepcionado. Pelo título desse post, parece que estou vendendo como utilizar essas estimativas para melhorar sua vida; porém no final da seção anterior pode dar a impressão de que estou dizendo que elas de nada servem para a SUA vida. Porque me dei ao trabalho de explicar detalhadamente como interpretar a incidência e o risco relativo, se no final das contas, eles são tão imprecisos que você não consegue utilizá-los?

Na realidade, meu objetivo com esse post é garantir que você tenha as informações adequadas para tomar as suas decisões. Quero que você entenda, mesmo que superficialmente, a quantidade de informações e suposições necessárias para que as estimativas possam ser calculadas, além de compreender o significado delas. Não estamos falando de uma coisa trivial como prever sua próxima compra na Amazon com os dados do seu histórico de compras. Estamos falando de modificar a sua vida ao abrir mão de coisas potencialmente importantes para você por causa de uma estimativa. Se você for fazer isso, é melhor saber de onde vem “a estimativa”⁶. Ela é uma estimativa escolhida entre várias estimativas possíveis. Utiliza um contexto entre vários contextos possíveis; foi gerada por um modelo, o qual foi escolhido entre vários modelos possíveis, e que leva em consideração somente algumas das variáveis importantes. Baseia-se em uma pesquisa utilizando uma metodologia, escolhida entre diversas metodologias possíveis.

Além disso, a estimativa se refere à chance de desenvolver câncer. Talvez fosse mais interessante alguma estatística relacionada ao tempo de vida. Porque no final das contas, todos vamos morrer. Talvez a questão mais importante seja quanto tempo vamos viver, e não necessariamente qual doença podemos adquirir. Dessa forma, conseguiríamos fazer escolhas levando em consideração uma informação mais tangível: “Você prefere ter, em média, mais um mês de vida, ou comer salgadinhos uma vez por semana?”.

No final das contas, a escolha sobre como usar essa informação é sua. As consequências das suas decisões serão suas, somente suas. Se o seu perfil é de buscar o risco zero, mesmo ele não existindo, então deixe de comer alimentos ultraprocessados. Se você acha mais importante ser feliz, não importa por quanto tempo, então coma alimentos ultraprocessados se você gosta deles, sem peso na consciência. Se você se posiciona entre esses dois extremos, a decisão é mais complexa. Não é óbvia nem exata nem objetiva. O melhor jeito, me parece, é você usar as estatísticas para decidir. Não deixe as estatísticas decidirem por você.